গগণ সাহেবের অফিসে তার মিটিং নেওয়ার কথা ছিলো সন্ধ্যা ৭ টায়। হঠাৎ তার বাসা থেকে ফোন আসে। তার ওয়াইফ কন্ডেন্সমিল্কের কৌটো কাটতে গিয়ে হাত কেটে ফেলেছে। তিনি দ্রুত বাসার দিকে যান। গিয়ে দেখেন আসলে তেমন কিছুই না। আজ তাদের এনিভার্সারি। তাই তাড়াতাড়ি তাকে বাসায় আনার জন্য ছোট্ট একটা মিথ্যে বলা হয়েছে। ওদিকে মিটিং ক্যান্সেল হওয়াতে অফিস আগেই শেষ হয়ে যায়। অফিস থেকে বের হয়ে শোভন আর গালিব ভাবে, এক ঘন্টা আগে যেহেতু অফিস শেষ হয়েছে। তাই বাসায় না গিয়ে তারা কোথাও আড্ডা দিবে। গালিবের বাইকে চড়ে তারা তাদের এক বন্ধুর বাসার দিকে রওনা দেয়। হাইওয়েতে বাইক জোড়ে রাইড করার ফলে ওভারটেকিং এর সময় পেছনের বাসের সাথে ধাক্কা লেগে ভয়াবহ দূর্ঘটনা ঘটে।
পুরো লেখাটি পড়তে না চাইলে ভিডিওটি দেখুন
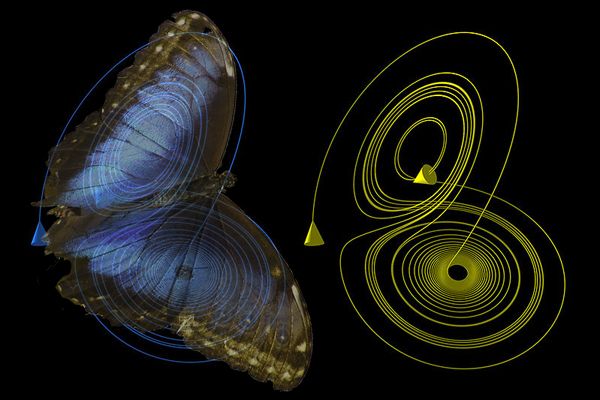
ঘটনা আবার পেছনের দিকে নিয়ে যাই। ধরুন গগণ সাহেবের ওয়াইফ কন্ডেন্সমিল্কএর কৌটা কাটতে গিয়ে হাত কাটলো না। গগণ সাহেবও মিটিং এট্যান্ড করলেন। অফিসও আর এক ঘন্টা আগে শেষ হলো না। এই কারণে গালিব আর শোভনও তাদের বন্ধুদের বাসায় যাওয়ার সিদ্ধান্ত নিলো না। রাস্তায় দূর্ঘটাওনাও ঘটলো না। অর্থাৎ দেখা যাচ্ছে সামান্য কন্ডেন্সমিল্কের কৌটো কাটতে গিয়ে রাস্তায় ভয়াবহ দূর্ঘটনার ঘটনা পুরোপুরি বদলে গেলো। আবার যদি গালিব আর শোভন বন্ধুর বাসায় ঠিকঠাক পৌছাতে পাড়তো, তাহলে ঘটনা সম্পুর্ন অন্যদিকে মোড় নিতো। এই যে ঘটনার সঙ্গে ঘটনার যে জটিলতা, একে বিজ্ঞানের ভাষায় ‘ক্যাওয়াস থিওরী’ বলা হয়। উপরের ঘটনা কাল্পনিক হলেও এটা সত্য যে এই পৃথিবীর প্রতিটা মানুষ একে অন্যের কাজ দ্বারা প্রভাবিত। একে সধারণত “বাটারফ্লাই ইফেক্ট”-ও বলা হয়।
‘আমেরিকান এসোসিয়েশন ফর দ্য অ্যাডভান্সমেন্ট অফ সায়েন্স’ এর ১৩৯ তম অধিবেশনে গণিতবিদ এবং আবহাওয়াবিদ ‘এডওয়ার্ড লরেঞ্জ’ একটি বিশেষ প্রশ্নের উত্থাপন করেছিলেন। প্রশ্নটি ছিলো এমন যে, ব্রাজিলে যদি কোনো একটি প্রজাপতি তার ডানা ঝাপটায়, তবে সেই ডানা ঝাপটানোর সুবাদে টেক্সাসে টর্নেডো হতে পারে কি না? প্রশ্নটি শুনে উপস্থিত সকলে তাকে পাগল ভাবতে শুরু করেছিলো। কারণ- প্রথমত, প্রজাপতির ডানা ঝাপটানোর কারণে আর যা-ই হোক, টর্নেডো হতে পারে না। দ্বিতীয়ত,
যদি টর্নেডো হয়েই থাকে, তবে ব্রাজিলে না হয়ে সেটা টেক্সাসে হবে কী করে!
যদিও প্রজাপতির পাখা ঝাপটানো নিয়ে লরেঞ্জ তার এই প্রশ্নে আসলে এটা বোঝাতে চাননি যে, আসলেই পৃথিবীর এক স্থানে প্রজাপতি ডানা ঝাপটালে আরেক স্থানে টর্নেডো হয়। বরং তিনি তার এই অদ্ভুত প্রশ্নের মাধ্যমে এটিই দেখাতে চেয়েছিলেন যে, কোনো বৃহৎ এবং জটিল সিস্টেমের ক্ষুদ্র পরিবর্তনের কারণে সিস্টেমের বৈশিষ্ট্য কতখানি বদলে যেতে পারে!
লরেঞ্জ আবহাওয়ার পূর্বাভাস দেয়ার জন্য একটি গাণিতিক মান ব্যবহার করেন, যার মান ০.৫০৬। এই মান আসলে আরো একটু বিস্তৃত ছিলো, অর্থাৎ দশমিকের পরে আরো সংখ্যা ছিলো। এর মান ছিলো ০.৫০৬১২৭। তিনি যখন দশমিকের পরে ছয় সংখ্যা নিয়ে গণনা করলেন, তখন একটি মান আসলো। কিন্তু যখন দশমিকের পরে তিন সংখ্যা নিয়ে গণনা করলেন, সেই ফলাফল ছিলো পূর্বের ফলাফলের থেকে অনেকখানি আলাদা। অথচ শুধু দশমিকের পরে কেবল তিন সংখ্যাই বাদ দেয়া হয়েছিলো, কিন্তু ফলাফলে দেখা গেলো অনেক পরিবর্তন।
এভাবে তিনি কম্পিউটার প্রোগ্রামে প্রায় ১২টি মান প্রদান করেন। মানগুলো ছিলো মূলত তাপমাত্রা, বাতাসের গতি, আর্দ্রতা এসবের। এর থেকে লরেঞ্জ এই সিদ্ধান্তে উপনীত হন যে, আবহাওয়ার পূর্বাভাসের ক্ষেত্রে মানের সামান্য পরিবর্তনের জন্য এর উপর যে প্রভাব পড়ে, সেটি মোটেও সামান্য নয়, বরং ব্যাপক। এভাবেই জন্ম নিলো ‘বাটারফ্লাই ইফেক্ট’ নামক ক্যাওয়াস থিওরী।
জাপানের নাগাসাকিতে যুক্তরাষ্ট্রের পারমাণবিক বোমা বিস্ফোরণের ঘটনার ভয়াবহতা আমরা সকলেই জানি। কিন্তু আসল ঘটনা হচ্ছে যে, মার্কিন পাইলটদের নাগাসাকিতে সেদিন পারমাণবিক বোমা ফেলার কথা ছিলো না। জাপানের আরেকটি শহর ‘কুরোকো’ তে সামরিক অস্ত্রঘাঁটি তাদের টার্গেট ছিলো।
কিন্তু যখন মার্কিন বোমারু বিমান কুরোকো শহরে বোমা ফেলার উদ্দেশ্যে উড়লো, তখন কুরোকোর আকাশে ছিলো মেঘ। পাইলটেরা এই মেঘ ভেদ করে অস্ত্রঘাঁটি কোনোভাবেই দেখতে পেলেন না। তারা তিনবার চেষ্টা করলেন টার্গেটে আঘাত হানার। কিন্তু শুধুমাত্র মেঘের কারণে সেটা সম্ভব হলো না। ফলে মার্কিন পাইলটরা সিদ্ধান্ত নিলেন নাগাসাকিতে বোমা ফেলার এবং সেটাই করা হলো।
সামান্য মেঘের কারণে কুরোকো শহর এই ভয়ংকর বোমা বিস্ফোরণের হাত থেকে রক্ষা পেলো। অপরদিকে এই সামান্য মেঘের কারণেই ‘নাগাসাকি’ মার্কিন পাইলটদের টার্গেট না হয়েও ধ্বংস হয়ে গেলো। এই যে সামান্য মেঘের কারণে দুই শহরের অবস্থা হলো দু’রকম, অথচ এরকম হওয়ার কথা ছিলো না, এখানেও কিন্তু এই বাটারফ্লাই ইফেক্ট দেখা যাচ্ছে।